Tunnel kinetic effect

    The tunnel kinetic effect is the effect of gaseous and liquid substances internal kinetic (thermal) energy vectors transformation, when these substances are located in the special tunnels, formed by the forces of a heterogeneous electric field.

    This effect makes possible to use internal kinetic energy of substance and it can be used practically in all applied areas of science and technology.

    We can refer to the request PCT/RU 2006/000589 “The method of electrical signal transformation into the acoustic oscillations and the poly-form electro-gas kinetic converter” as the example to the practical realization of this effect.

    Because of the space limitation of this note the phenomena, which occur at the atomic level, undoubtedly deserving separate attention and explanation in an independent document, are not examined in it.

    In prospect, this phenomenon will possibly specify our understanding of different processes, which occur also in living nature; since we all live in the electric field, formed by the terrestrial globe and the ionosphere, and this field's tensity is such, that not to consider it is simply impermissible.

Introduction

 

“Theory produces the greater impression, the simpler is its precondition, the more different is the phenomenon between which it establishes connection, the vaster is the region of its application”

Albert Einstein

    In 1827 English botanist Brown discovered permanent motion or chatter of the small particles diffused in a liquid in a plant preparations under the microscope. Afterwards it turned out that this property is not limited to living nature, but is inherent to all liquid and gaseous substances. It is possible to consider proven that there is a invisible and incessant motion of the smallest particles (molecules, atoms) in the completely steady liquid or gas. This motion never ceases and it is tightly connected with the thermal condition of liquid or gas: with an increase of temperature the intensity of Brownian motion grows.

    Observing Brownian particle motion at different temperatures, it is possible to establish the direct connection of average kinetic energy Ek of gas (liquid) molecules with the temperature T:

. (1)

where

T – the temperature, calculated of absolute zero and equal to temperature according to Celsius, increased to 273.16°;
u – speed;
k – universal constant, identical for all substances in any state (Boltzmann constant).
k = 1.3802 x 10-23 J/deg. (2)

    Kinetic energy can be represented as the sum of the kinetic energies, created by the velocity components along three mutually perpendicular coordinate axes1 X, Y, Z (Fig. 1):


Fig. 1

(3)

    Since all three directions of speed are equally probable, then it is possible to assume for the average kinetic energy:

(4)

and, therefore, for the average kinetic energy in one determinate direction X, Y or Z:

(5)

1 for the presentation simplification, the monatomic molecule model is used.

Velocities of molecules in the thermal agitation

    In a gas, the molecule moves rectilinearly with the definite speed, until it meets another molecule on its path. As a result of interaction between them, directions and velocities of both molecules are changed. In this case, if one of the molecules reduces its speed, then another moves more rapidly. Certainly, it is difficult to trace these changes in the speeds in diffirent directions, rapidly following each other. But, as a result of prolonged process of permanent interaction, the specific percentage of particles at velocity, close to the definite value u1, will fare among the numerous molecules of gas, some another percentage of particles at velocity, close to u2, will also fare among them, etc. Through a certain time interval, particles at velocities, close to u1, will obtain other velocities, but as many other molecules will move at velocity, close to u1 (as a result of interactions); from the total number – N – of the molecules, which are consisted in the given volume of gas, let us consider a certain number of molecules ΔN, which are located in the volume ΔV and which possess the velocities within the range from u1 to u1 + Δu. This number is not strictly constant, it can first be increased, then reduced, but the greater is ΔN, the less are possible deviations in comparison with ΔN. In the normal conditions in gases, when not only N, but also ΔN it is great, it is possible to speak about value ΔN at the given moment with high definiteness. Even in very small volumes ΔV of gas in the normal conditions, still many particles are contained, and, with not very small interval of  velocities δu, the value ΔN still will be great. Computations show that:

(6)

(the Maxwell-Boltzmann distribution). Here k – Boltzmann's constant, A – a certain constant factor, and E is the sum of kinetic energy of the molecule mu2/2 and its potential energy (P).

    We can redefine equation (6) in this form:

(7)

    If potential energy P is identical for all molecules of gas, then value e-P/kT will be constant, and the expression (7) is assigned the following form:

(8)

     Equal number ΔN of the particles, possessing these velocities, will lay in equal volumes, and the total number of particles n at all possible velocities will be also equal in identical volumes ΔV.

The channel form influence on the gas molecules motion velocities

    Considering all that was presented above (the classical kinetic theory of gases), let us try to make  several theoretical experiments, which consist of a comparative evaluation of kinetic parameters of  equal volumes of gas, which is placed in the volumetric structures of a various forms.


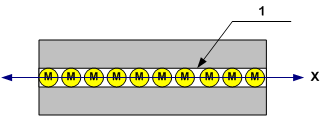
Fig. 2

    Figure 2 depicts the conventional, ideal channel (mono-drohm tunnel2 – 1), which has diameter commensurate with the dimensions of gas molecule (M), lengthwise which a certain quantity of gas molecules can be placed. Conventional, ideal channel in this case is a certain physical abstraction that doesn't have inherent characteristics and intended for limiting molecules thermal agitation freedom degrees (in such structure of the channel, molecules can have only one degree of freedom – along the X-axis).


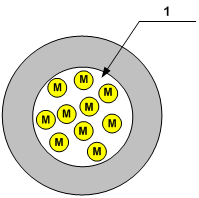
Fig. 3

    The figure 3 depicts the conventional, ideal sphere, which has volume equal to the volume of channel (Fig. 2) and contains equal quantity of gas molecules (M).

    In accordance with the expression (3) let us calculate kinetic energy of the gas, located in the volume of this sphere:

where n  – quantity of gas molecules being contained in the given volume, or:

    Let us try to calculate kinetic energy of the gas, included in the ideal channel of the equal volume:

where uy and uz = 0, since the molecules are limited in their possibilities to move in these directions.

    We obtain:

at constant temperature T this equation  contradicts the energy conservation law. Let us try to calculate this equation. Considering the constancy of molecular mass, their total quantity and the constancy of temperature conditions, we have an opportunity to solve this equation only due to use of the molecule motion velocity increase coefficient. Simple computations show that:

(9)

Conclusion:

    The thermal movement velocity of molecule, enclosed in the channel, whose diameter corresponds to the size of the molecule itself, is increased by the coefficient s = √n, where n – the gas molecule freedom degrees number. For the monatomic gas, for example, helium, argon, neon and other s == 1.73205080756.

2 mono-drohm tunnel – nanochannel, in which only one path of molucule motion is feasible (from the Greek. μόνος – one, only and δρόμος – way, route).

Statistical laws

    Properties of gas are determined by the fact that it is a system consisting of the immense number of particles. What methods can be used to study the properties of gases and other questions of molecular physics, which always deals with similar systems?

The following ways can be used to solve the problems of molecular physics:

    The oldest method – an experimental measurement of the values that characterize state of the object, its density, pressure, temperature, form – and the establishment of laws linking these values. The most radical path to understanding of these laws is transition from the total observation to study of the elementary phenomena mechanism lying at its base – object particles thermal motion. However, this path was immediately discovered to be unattainable because of a enormous quantity of particles and randomness of their motion. Furthermore, a problem solve is also unrealizable because separate particles are not distinguished, and their set cannot be considered as a simple sum of particles.

   The closer examination proves that solution of this problem is not even necessary – it is adequately replaced by the establishment of statistical laws. It is almost impossible to discover what kinetic energy is possessed by a concrete molecule, but the value of average kinetic energy of all object molecules can be estimated from object temperature, using, for example, the equation (1).

    A complex phenomena molecular mechanism statistical examination serves as one of the most common methods of physics; besides it, the probabilistic methods of determining the substance state are also used.



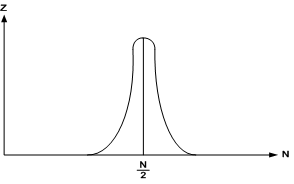
Fig. 4

    Figure 4 depicts the diagram on which the distribution of molecules between two halves of volume is shown.

    Boltzmann had computed, that even for a relatively small volume of 1 cm3, the probability of simultaneous location of all gas molecules in one half of this volume is expressed by the number, which is of the probability, that all of them are uniformly distributed in both halves. The more molecules are enclosed in this system, the less is the probability of digression from the described distribution.

The temperature change

As it was shown above, one molecule freedom degree accords to the energy of  and it is necessary to clarify, how can the following equality be observed:

???

    From the resulting expression it is evident that for abiding this equality the temperature of gas in a nanochannel must grow in 3 times (it must be more than 500 degrees Celsius). However, as a result of carried out experiments such increase in the temperature was not discovered; this can be explained by the construction of kinetic converter and by the symmetry of the sound, harmonic signal transformation process in this converter (see Fig. 6). A change in the temperature is completely confirmed with the use of other constructions (see Fig. 7).

Some terms and physical values

3 from the Greek πολύ – many, δρόμος – way, route.

How does the Electro- Gas-kinetic Converter work



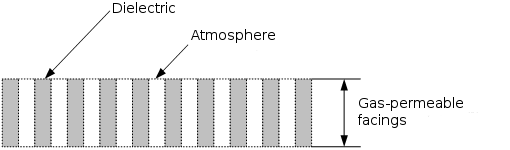
Fig. 5

    Figure 5 depicts a converter operating element cut fragment, which consists of the alternating, perforating microchannels (nanochannels) containing the air, and the substance itself (dielectric), which forms the given three-dimensional construction.



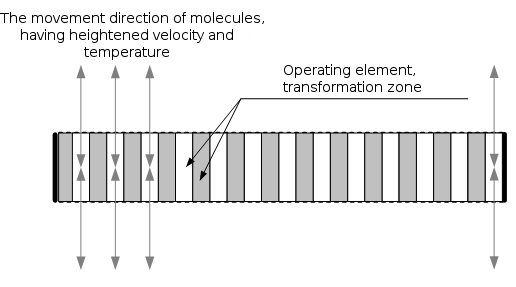
Fig. 6

    Figure 6 schematically shows a cut of the converter, which realizes a symmetrical-filtrating construction that works as it is written below.

    During the supplying gas-permeable facings of the converter with the required electrical signal, kinetic tunnels begin to appear in the working element; in that tunnels, the gas (liquid) kinetic energy conversion factor is a function of the supplied signal amplitude. As a result of their appearance, the molecules thermal movement velocity vectors transformation occurs in the plane that is perpendicular to the emitter surface. Molecules, that have an increased velocities, escape from the working element and, transmitting their energy to ambient air, create acoustic oscillations. These molecules have heightened temperature and free run about 3-6 mm. With the decrease of the voltage forming kinetic tunnels, they are filtered back in the working element and there doesn't occur  any observable significant change in the temperature of converter itself or environment. This phenomenon can be observed visually using photo or video equipment that enables capturing of thermal radiation.

    As it was mentioned above, the molecule motion velocity increase coefficient depends of molecule freedom degrees quantity (n), determined by the structure of substance and is equal to .

    The mechanism of tunnel kinetic effect and methods of kinetic tunnels designing can be described more detailed only with the examination of phenomena that are taking place at the level of substance atomic structure, which exceeds the scope of that article.

    The mock-ups allowed achieving the sound signal level up to 130 dB. Theoretically, this method of creating acoustic oscillations doesn't limit the level of sound signal and the dynamic range of acoustic system. The maximum coefficient of efficiency of the converter operating with the air can reach 80% (from the kinetic energy of air, which is used as the operating environment).

    The working mock-up of acoustic converter (of filtrating-reflective construction), which realizes SNEGS technology, is shown in the photographs given below.

 

The converter, which realizes the flowing method of using the gas (liquid) kinetic energy, working principles



Fig. 7

    Figure 7 depicts the cut of tunnel kinetic converter, which realizes the flowing (direct-flow) method of gas (liquid) kinetic energy conversion. Converter works as it is written below.

    In the conversion zone, the operating substance (gaseous, liquid) internal kinetic energy vectors transformation occurs under the action of electric field; this substance obtains the acceleration, accompanied by an increase of kinetic flow temperature at the device output and by cooling and pressure lowering in the conversion zone. In accordance with the Maxwell-Boltzmann distribution,  a substance will permanently enter the operating zone from the space surrounding the converter, the internal kinetic energy vector of which will be continiously transformed. With the complete kinetic energy utilization of 1 cubic meter of air having the temperature of 0°C, the power of this converter will be not less than 220 kW or 300 hp in 1 second (in the liquids, where “the packing density” of molecules is several degrees above, this power it will amount hundreds of thousands of kW).

Conclusion

    Humans has begun to use a potential energy of different substances for his various needs long time ago, basically for obtaining the energy. The discovery of tunnel kinetic effect and the practical realization of various devices with its use makes it possible to use internal kinetic energy of substances, among the boundless ocean of which we are located.

    Simple calculations show that the reserves of this renewable energy source are truly limitless and its use does not require the construction of dams and turning of rivers, the source of this energy is located at any geographical point of our planet and is available to any country and people.

Saint Petersburg, Russia, 2007.
Dmitriev S. P. – the investigator.




Hosted by uCoz