Туннельный кинетический эффект

Туннельный кинетический эффект – это эффект преобразования векторов внутренней кинетической (тепловой) энергии газообразных и жидких веществ находящихся в специальных туннелях, образованных силами неоднородного электрического поля.

Данный эффект позволяет использовать внутреннюю кинетическую энергию вещества и может применяться практически во всех прикладных областях науки и техники.

Примером практической реализации данного эффекта может служить заявка PCT/RU 2006/000589 «Способ преобразования электрического сигнала в акустические колебания и полиформный электрогазокинетический преобразователь».

В связи с ограниченным объемом данной записки в ней не рассматриваются явления, происходящие на атомном уровне, которые, безусловно, заслуживают отдельного внимания и пояснения в самостоятельном документе.

В дальнейшем, возможно, данное явление позволит уточнить наше понимание различных процессов, происходящих и в живой природе, поскольку все мы живем в электрическом поле, образованном земным шаром и ионосферой, а величина напряженности этого поля такова, что не учитывать его просто не допустимо.

Введение

«Теория производит тем большее впечатление, чем проще её предпосылки, чем различнее явления, между которыми она устанавливает связь, чем обширнее область её применения»

Альберт Эйнштейн

В 1827 году английский ботаник Броун обнаружил в растительных препаратах под микроскопом постоянное движение или дрожание мелких частиц, взвешенных в жидкости. Впоследствии оказалось, что это свойство не ограничивается живой природой, а присуще всем жидким и газообразным телам. Можно считать доказанным, что в совершенно спокойной жидкости или газе существует невидимое и непрекращающееся движение мельчайших частиц (молекул, атомов). Это движение никогда не прекращается и тесно связано с тепловым состоянием жидкости или газа: с повышением температуры интенсивность Броунова движения возрастает.

Наблюдая Броуново движение частиц при различных температурах, можно установить прямую связь средней кинетической энергии E_k молекул газа (жидкости) с температурой Т:

(1)

где

Т - температура, отсчитываемая от абсолютного нуля и равная температуре по Цельсию, увеличенной на 273,16 градуса;
u - скорость;
k - универсальная постоянная, одинаковая для всех веществ и в любых состояниях (постоянная Больцмана)

k = 1.3802 x 10^-23 дж/град.

(2)

Кинетическую энергию можно представить как сумму кинетических энергий, создаваемых составляющими скорости по трем взаимно перпендикулярным осям координат¹ X, Y, Z (Рис. 1):

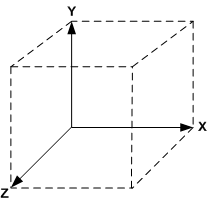
Рис.1

(3)

Так как все три направления скорости одинаково вероятны, то для средней кинетической энергии можно положить:

(4)

и, следовательно, для средней кинетической энергии движения в одном определенном направлении X,Y или Z

(5)

1 Для упрощения изложения используется одноатомная модель молекулы

Скорости молекул в тепловом движении

В газе молекула движется с определенной скоростью прямолинейно, пока не встретит на своем пути другую молекулу. В результате взаимодействия между ними направления и величины скоростей обеих молекул изменяются. Если одна из молекул при этом уменьшает свою скорость, то другая движется быстрее. Конечно, трудно проследить за этими, быстро следующими друг за другом, изменениями скоростей то в одном, то в другом направлении. Но в результате длительного процесса постоянного взаимодействия, среди многочисленных молекул газа окажется определенный процент частиц со скоростями, близкими к какой-нибудь скорости u1, какой-то другой процент частиц со скоростями, близкими к u2 и т.д. Через некоторый промежуток времени молекулы, обладающие скоростями, близкими к u1, получат иные скорости, но зато столько же других молекул в результате взаимодействия будут двигаться со скоростями, близкими к u1; из общего числа N молекул, заключающихся в данном объёме газа, рассмотрим некоторое число молекул ΔN, находящихся в объеме ΔV и обладающих скоростями, лежащими в пределах от u1 до u1 + Δu. Это число не строго постоянно, оно может то увеличиваться, то уменьшаться, но чем больше само число ΔN, тем меньше случайные отклонения по сравнению с ΔN. При обычных условиях в газах, когда не только N, но и ΔN очень велико, можно с большой определенностью говорить о величине ΔN в данный момент. Даже в очень малых объемах ΔV газа при обычных условиях содержится еще очень много частиц и, при не очень малом интервале скоростей Δu, величина ΔN будет ещё очень велика. Вычисления показывают, что

(6)

(закон распределение Максвелла-Больцмана). Здесь k – та же постоянная Больцмана, A – некоторый постоянный множитель, а E представляет собой сумму кинетической энергии молекулы mu²/2 и её потенциальной энергии (P)

Уравнение (6) мы можем переписать в таком виде:

(7)

Если потенциальная энергия P одинакова для всех молекул газа, то величина e^-P/kT будет постоянной, и выражение (7) примет следующий вид:

(8)

В равных объёмах будет заключаться равное число ΔN частиц, обладающих данными скоростями, а общее число частиц n всевозможных скоростей будет также одинаково в одинаковых объёмах ΔV.

Влияние формы канала на скорости движения молекул газа

Принимая во внимание и учитывая изложенное выше (классическую кинетическую теорию газов), попробуем поставить несколько теоретических экспериментов, заключающихся в сравнительной оценке кинетических параметров равных объемов газа, располагающегося в объемных структурах, имеющих различную форму.

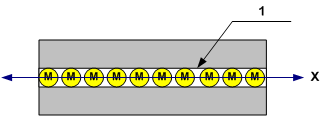
Рис.2

На рисунке 2 изображен условный, идеальный канал (монодромный туннель² - 1), имеющий сечение соизмеримое с размерами молекулы (М) газа, по длине которого может располагаться некоторое количество молекул газа. Условный, идеальный канал в данном случае, это некоторая физическая абстракция, не имеющая собственных характеристик и предназначенная для ограничения степеней свобод теплового движения молекул (в подобной, идеальной структуре канала молекулы могут иметь только одну степень свободы – вдоль оси Х).

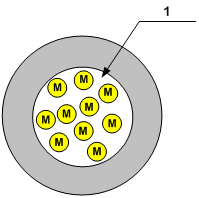
Рис.3

На рисунке 3 изображена условная, идеальная сфера, имеющая объем равный объему канала (Рис.2) и вмещающая равное количество молекул (М) газа.

В соответствии с выражением (3) рассчитаем кинетическую энергию газа, расположенного в объеме данной сферы:

где n – количество молекул газа содержащихся в данном объеме, или:

Попробуем рассчитать кинетическую энергию газа, заключенного в идеальном канале равного объема:

где u_y и u_z = 0, поскольку молекулы ограничены в своих возможностях двигаться в этих направлениях.

Получаем:

что, при неизменной температуре Т - противоречит закону сохранения энергии. Попробуем рассчитать данное уравнение. Учитывая постоянство массы молекул, их общее количество и постоянство температурного режима, имеем возможность решить данное уравнение только за счет применения коэффициента увеличения скорости движения молекулы. Простые вычисления показывают:

(9)

Вывод:

Скорость теплового движения молекулы, заключенной в канал, сечение которого соответствует размеру самой молекулы, увеличивается на коэффициент s = √n, где n – количество степеней свободы молекулы. Для одноатомного газа, например, - гелия, аргона, неона и др. s = = 1.73205080756.

2 монодромный туннель – наноканал, в котором возможен только один путь движения молекулы (от греч. μόνος – один, единственный и δρόμος – дорога, путь).

Статистические законы

Свойства газа определяются тем, что он является системой, состоящей из громадного числа частиц. Какими же методами можно изучать свойства газов и другие вопросы молекулярной физики, которая всегда имеет дело с подобными системами?

Проблемы молекулярной физики могут решаться следующими путями:

Феноменологическим описанием;
Изучением детального механизма;
Статистическими методами.

Старейший по времени прием – опытное измерение величин, характеризующих состояние тела, - его плотности, давления, температуры, формы, и установление законов, связывающих эти величины. Наиболее радикальный путь к пониманию этих законов – это переход от суммарного наблюдения к изучению лежащего в его основе механизма элементарных явлений – теплового движения частиц тела. Этот путь, однако, сразу оказался недостижимым из-за огромного количества частиц и хаотичности их движения. Кроме того, подобная детальная задача неосуществима и потому, что отдельные частицы неразличимы, и их совокупность нельзя рассматривать как простую сумму частиц.

При ближайшем рассмотрении оказывается, что решение такой задачи и не нужно – она с полным успехом заменяется установлением средних статистических закономерностей. Практически невозможно узнать какой кинетической энергией обладает конкретная молекула, но о величине средней кинетической энергии всех молекул тела можно судить по его температуре, исходя, например, из уравнения (1).

Статистическое рассмотрение сложного молекулярного механизма явлений служит одним из наиболее распространенных методов физики, кроме него используются вероятностные методы определения состояния вещества.

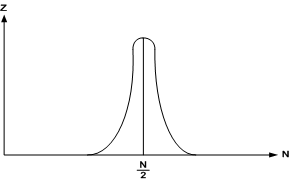
Рис.4

На рисунке 4 изображена диаграмма распределения молекул между двумя половинами объема.

Как вычислил Больцман, даже для сравнительно небольшого объема в 1 см³ вероятность одновременного нахождения всех молекул газа в одной половине этого объема выражается числом, составляющим вероятности их равномерного распределения по обеим половинам. Чем больше молекул заключено в данной системе, тем меньше вероятность отступления от рассмотренного распределения.

Изменение температуры

Как указывалось выше, на одну степень свободы молекулы приходится энергия, равная и необходимо пояснить каким образом может соблюдаться равенство:

???

Из приведенного выражения видно, что для соблюдения этого равенства температура газа в наноканале должна возрасти в 3 раза (должна составлять более 500 градусов Цельсия). Однако, в результате проведенных экспериментов столь значительное увеличение температуры не было обнаружено, что можно объяснить конструкцией кинетического преобразователя и симметричностью процесса преобразования звукового, гармонического сигнала в данном преобразователе (см. Рис. 6). При использовании других конструкций (см. Рис. 7) изменение температуры полностью подтверждается.

Некоторые определения и физические величины

Рабочий элемент, матрица, зона преобразования - пространственная структура, имеющая заданные геометрические размеры, физические свойства и электромеханические характеристики, предназначенная для придания газовой среде требуемых кинетических свойств, в течение установленного срока эксплуатации.
Монодромный туннель (канал) – пространственная структура, ограничивающая свободное перемещение молекул газа (жидкости) в любых произвольных направления и устанавливающая для такого движения только один, заранее определенный маршрут.
Полидромный³ туннель (канал) - пространственная структура, ограничивающая свободное перемещение молекул газа (жидкости) в любых произвольных направления и устанавливающая для такого движения несколько, заранее определенных маршрутов.
SNEGS – Synchronous Nano- Electro- Gas-kinetic System – Синфазная Нано-, Электро-, Газокинетическая Система.
При атмосферном давлении и температуре 0 градусов Цельсия в одном кубическом сантиметре газа находится 2,68 х 10¹⁹ молекул.
Кинетический диаметр молекулы азота составляет 3,7 х 10^-10 м.
В составе воздуха, являющегося сложной смесью различных газов содержится около 70% азота.
Один кубический сантиметр азота, при нормальном атмосферном давлении (760 мм рт.ст.) и температуре 0 градусов Цельсия обладает кинетической энергией 0,2526 дж.

3 от греч. πολύ – много, δρόμος – дорога, путь.

Как работает электрогазокинетический преобразователь

Рис.5

На рисунке 5 условно изображен разрез фрагмента рабочего элемента (матрицы, тела) преобразователя, состоящий из чередующихся, сквозных микроканалов (наноканалов), содержащих воздух и самого вещества (диэлектрика), образующего данную пространственную конструкцию.

Рис.6

На Рис. 6 схематично показан разрез преобразователя, реализующего симметрично–фильтрационную конструкцию, работающую следующим образом.

При подаче на газопроницаемые обкладки преобразователя требуемого электрического сигнала, в теле рабочего элемента начинают возникать кинетические туннели, коэффициент преобразования кинетической энергии газа (жидкости) в которых, является функцией от амплитуды подаваемого сигнала. В результате образования данных туннелей, происходит преобразование векторов скоростей теплового движения молекул в плоскости, перпендикулярной поверхности излучателя. Молекулы, имеющие повышенные скорости, вылетают из тела рабочего элемента и, передавая свою энергию окружающему воздуху, создают акустические колебания. Эти молекулы имеют повышенную температуру и свободный пробег около 3-6мм. При уменьшении напряжения, под действием которого происходит формирование кинетических туннелей, они фильтруются обратно в тело рабочего элемента и значительное изменение температуры самого преобразователя и окружающей среды не наблюдается. Данное явление можно наблюдать визуально, применив фото или видео аппаратуру, позволяющую фиксировать тепловое излучение.

Как упоминалось выше, коэффициент увеличения скорости движения молекулы зависит от количества степеней свободы молекулы (n), определяемый строением вещества и равен .

Более детально, механизм туннельного кинетического эффекта и способы создания кинетических туннелей может быть описан только при рассмотрении явлений происходящих на уровне атомного строения вещества, что выходит за рамки настоящей статьи.

Изготовленные модели (макеты) позволяли получать уровень звукового сигнала до 130 дБ. Теоретически, данный способ получения акустических колебаний, не накладывает ограничений на уровень звукового сигнала и динамический диапазон акустической системы. Максимальный КПД преобразователя работающего с воздухом может достигать 80% (от кинетической энергии воздуха, использующегося в качестве рабочей среды).

На приведенных ниже фотографиях показана действующая модель акустического преобразователя (фильтрационно–отражательной конструкции), реализующего SNEGS технологию.

Работа преобразователя, реализующего проточный метод использования кинетической энергии газа (жидкости)

Рис.7

На Рис. 7 показан разрез туннельного кинетического преобразователя, реализующего проточный (прямоточной) способ преобразования кинетической энергии газа (жидкости). Преообразоаватель работает следующим образом.

В зоне преобразования, под действием сил электрического поля, происходит преобразование векторов внутренней кинетической энергии рабочего вещества (газообразного, жидкого), которое получает ускорение, сопровождаемое увеличением температуры кинетического потока на выходе устройства и охлаждением и понижением давления в зоне преобразования. В соответствии с законом распределения Максвелла-Больцмана в рабочую зону постоянно будет поступать вещество пространства, окружающего преобразователь, вектора внутренней кинетической энергии которого, будут непрерывно преобразовываться. При полном использовании кинетической энергии 1 кубического метра воздуха, имеющего температуру 0 градусов Цельсия, за 1 секунду, мощность такого преобразователя составит не менее 220 кВт или 300 л.с. (в жидкостях, где «плотность упаковки» молекул на несколько порядков выше эта мощность будет составлять сотни тысяч кВт).

Заключение

Человек давно использует потенциальную энергию различных веществ для самых разнообразных своих нужд и, в первую очередь, для получения энергии. Открытие туннельного кинетического эффекта и практическая реализация разнообразных устройств с его использованием позволяет использовать внутреннюю кинетическую энергию веществ, среди безбрежного океана которой мы находимся.

Простые расчеты показывают, что запасы этого возобновляемого источника энергии поистине безграничны и её использование не требует строительства плотин и поворота рек, источник этой энергии распологается в любой географической точке нашей планеты и доступен любому государству и народу.

г. Санкт-Петербург 2007г.
Дмитриев С.П. – исследователь.